Cette partie du forum n’est pas compatible avec les bloqueurs publicitaires
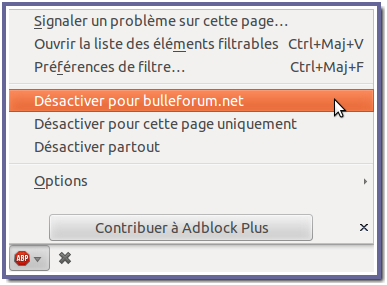
Félicitations à vous, de préférer les accès payants plutôt que la gratuité par la publicité, c’est honnorable et cohérent de votre part. Malheureusement, l’accès payant par micropaiement (qui serait d’environ 1 cent pour 20 pages consultées) n’est pour l’instant pas encore mis en place, et l’accès gratuit sans publicité, est réservé aux membres actif(ve)s du forum. En attendant, si vous souhaitez poursuivre votre visite chez nous, vous pouvez ajouter le site à votre liste blanche, ou encore mieux, désactiver le bloqueur partout. Pour ajouter le site à votre liste blanche, pour Firefox (similaire pour les autres navigateurs), rendez‑vous en bas à gauche de la fenêtre de votre navigateur, et cliquez sur le menu comme dans l’exemple de l’image ci‑dessous, puis rechargez la page, en appuyant sur F5.
|
|
|
| Auteur | Message |
|---|---|
|
Administrateur
|
Suite du précédent message, avec une réponse à la seconde question du paragraphe cité.
Ce qui est dit dans ce message est susceptible de devoir être complété et est sous réserve. Hibou a écrit : […] Et si le terme posé en hypothèse, B, est unifiable avec la tête d’une règle mais contredit la règle ? On sait en effet, que l’unification d’un terme avec la tête d’une règle, ne garantit pas que la règle sera vérifiée, à moins que le corps de la règle ne soit vide. Et si l’hypothèse est une conjonction au lieu d’un unique terme ? […] Jusqu’ici, unifier un terme A et un terme B, était la même chose qu’unifier le terme B et le terme A. Sans le dire, une distinction est apparue. L’unification n’est plus toujours symétrique, depuis qu’a été introduite la notion de couverture des cas. Quand à partir de l’hypothèse ⟦(nat N)⟧ est créé le cas (nat (s N_2)) avec N lié à (s N_2), la règle été supposée vérifiée. Mais pourquoi ? À cette question il sera répondu un peu plus loin. Dans le précédent exemple, le terme en hypothèse a la même forme que l’unique terme du corps de la règle représentant un cas. Ça peut être perturbant et c’est un cas particulier, ce qui peut être dangereux, alors pour la suite, un autre exemple va être choisi. On va reprendre avec l’exemple de la relation poly, qui était : §d0 (digit 0). §d1 (digit 1). §d2 (digit 2). §poly-b (poly (p N)) : (digit N). §poly-s (poly (p M N)) : (poly M) & (digit N). Disons que maintenant, on va envisager les cas possibles de l’hypothèse ⟦(poly P)⟧ ; il y en a deux. On va s’intéresser au premier, celui de la règle §poly-b. Le P de l’hypothèse va être lié à (p N) et l’hypothèse ⟦(digit N)⟧ sera produite. La liaison de P à (p N) vérifie‑t‑elle la règle §poly-b ? La réponse pourrait être que oui, puisqu’on a l’hypothèse ⟦(poly P)⟧, mais poly peut être vérifiée par l’autre règle, pas nécessairement celle‑ci et on sait qu’il ne suffit pas d’unifier un terme avec la tête d’une règle pour que la règle soit vérifiée. Pourtant, si on veut représenter ce cas, il faut que l’hypothèse ⟦(poly P)⟧ puisse le représenter. La question devrait alors être reformulée autrement : l’hypothèse ⟦(poly P)⟧ est‑elle en accord avec la liaison de P à (p N) et l’hypothèse produite, ⟦(digit N)⟧ ? La règle dit que pour vérifier (poly (p N)), il faut vérifier (digit N), et (digit N) est posé en hypothèse. Ors, P est lié à (p N), donc l’hypothèse ⟦(poly P)⟧ correspond à (poly (p N)), même si ce terme n’est pas une hypothèse (pour une règle représentant un cas, le corps de le règle est posé en hypothèse, pas la tête de la règle). L’hypothèse est bien unifiée avec la tête de la règle et l’hypothèse produite vérifie la règle. Oui, mais si on lie par exemple P à (p (abc def)), l’hypothèse pourrait toujours être unifiée avec la tête de la règle, mais la règle ne serait plus vérifiée, n’est‑ce pas ? Alors ça ne marche pas toujours, ça se voit. Oui, c’est justement pour cette raison qu’on ne liera pas P à n’importe quoi. On sait qu’un terme peut être vérifié par une hypothèse correspondante. Un cas particulier n’a pas été souligné, c’est celui où au lieu de certains termes seulement, tous les termes du corps d’une règle, sont vérifiés par une hypothèse. Depuis que les hypothèses ont été introduites, le langage a implicitement une inférence de la forme ⟦A⟧ ==> B, où A reprend les termes du corps d’une règle en les posant tous en hypothèse, et B, est la tête de la règle correspondante. Note : pour simplifier, les hypothèses prises en exemple ici sont toujours des termes seuls, mais elles peuvent être des conjonctions de termes. Si une règle est réalisable, c’est que son corps est réalisable. Le corps de la règle, quand il est posé en hypothèse, représente une solution générale de la règle (à ne pas interpréter trop hâtivement non‑plus, c’est une représentation, pas une méthode de résolution). On ne peut cependant pas poser la tête de la règle en hypothèse pour la seule raison d’avoir le corps de la règle en hypothèse, parce que la tête de la règle, peut correspondre à d’autres règles aussi. Par exemple si on a B : A1 et B : A2, même si avec l’hypothèse ⟦A1⟧ on peut vérifier un B, on ne peut pas poser B en hypothèse, parce qu’il existe une autre règle pour B. Le terme B vérifié par ⟦A1⟧, aurait ses variables liées comme dans le terme A1 de l’hypothèse, c’est à dire typiquement liées à des généralités. Mais même si le terme B porte sur des variables représentant toutes des généralités, on ne peut pas pour autant le prendre pour une hypothèse. Donc avec ⟦A1⟧, on peut vérifier un terme B tel qu’il apparaît comme tête de la règle B : A1. Mais c’est cohérent seulement si les variables de ce B, sont liées en vertu de ⟦A1⟧. Si les variables de ce B ne sont pas modifiée, on a la certitude que la règle est vérifiée. On peut unifier un terme avec ce B, si on ne modifie pas la moindre de ses variables, même indirectement. On reprend la question d’avant le précédent paragraphe. On a voulu poser un cas de ⟦(poly P)⟧. Ce cas est celui de la règle (poly (p N)) : (digit N), nommée §poly-b. Après avoir posé ⟦(digit N)⟧ en hypothèse, qui est le corps de la règle §poly-b, on a put vérifier un terme (poly (p N)), qui est la tête de la règle §poly-b. Quand on a unifié le terme de l’hypothèse ⟦(poly P)⟧, avec (poly (p N)), on a lié la variable P de l’hypothèse à (p N). Aucune variable du terme (poly (p N)), n’a été modifiée. Si on liait P à (p (abc def)) et qu’on unifiait ensuite (poly P) à (poly (p N)), il faudrait lier N à (abc def). On modifierait la variable N du terme (poly (p N)). C’est justement cette liaison qui ne doit pas être permise, parce que ce N doit rester inchangé, pour que (poly (p N)) soit tenu pour vérifié par ⟦(digit N)⟧. Dit d’une manière plus concise et plus formelle, si on a une hypothèse ⟦H⟧, pouvant correspondre à plusieurs règles et qu’on veuille couvrir chacun de ces cas, pour chaque cas représenté par une règle A : B, le corps B est posé en hypothèse, se faisant, les variables de A sont liées d’après B, puis le terme H est unifié avec le terme A, avec A constant, c’est à dire que aucune de ses variables ne peut être changée. L’hypothèse ⟦B⟧ est un cas du ⟦H⟧ d’origine, et ce cas, en plus d’être représenté ⟦B⟧, est aussi représenté par l’hypothèse ⟦H⟧ dérivée, où H est lié après unification avec A. Ce n’est pas la même chose que poser A en hypothèse, même si ça semble l’être ; un prochain message expliquera pourquoi. Le nouveau ⟦H⟧ remplace le précédent, dans la branche représentant le cas. La dernière phrase du précédent paragraphe, corrige une erreur que j’ai dite précédemment en parlant de conserver l’hypothèse d’origine dans la branche représentant le cas. C’était intuitivement assez correcte, mais formellement inexacte. C’est une hypothèse lui correspondant qui lui est substitué. Conserver l’hypothèse d’origine ne serait même pas possible, comme toutes les références à cette hypothèse seraient avec les variables apparaissant dans cette hypothèse, et ces variables seraient liés comme décrit plus haut, dans toute la branche représentant le cas. Ce n’est pas encore tout à fait tout. On entre dans une branche pour vérifier quelque chose dans ce cas, et on doit le vérifier pour plusieurs cas. Si la vérification échoue pour cette branche, elle échoue tout‑court et il n’est pas tenté de vérifier les autres cas, puisque la généralité ne serait pas vérifiée. Si la branche est vérifiée, les autres branches le sont de la même manière. À ce moment là, l’hypothèse d’origine est reprise pour entrer dans une nouvelle branche, en lui substituant à nouveau une hypothèse correspondante, pour cette branche. L’hypothèse d’origine peut être oubliée ou pas, c’est un détail technique, ça dépend de si les cas sont tous produits avant de les vérifier ou pas. L’important est que pour chaque branche, ce n’est pas l’hypothèse d’origine qui est visible, mais celle qui lui est substituée, une par branche. Reste encore une question en suspend. Comment est déterminée la liste des cas devant être couvert. Pour savoir si une règle est applicable à un terme, on unifie le terme avec la tête de la règle et ensuite on vérifie le corps de la règle. Avec les branches représentant les cas, selon la méthode décrite dans ce message, c’est différent. Le corps de le règle est posé en hypothèse, puis l’hypothèse est unifiée avec la tête de la règle maintenue constante (la tête de la règle). Si par exemple une hypothèse est ⟦(nat (s (s N)))⟧, quels sont les cas devant être couverts pour s’assurer de faire une vérification en général, pour la généralité que représente cette hypothèse ? En oubliant ce qui a été dit dans ce message et en revenant à l’unification ordinaire, (nat (s (s N))) serait unifiable avec (nat (s N_2)) ou N_2 serait lié à (s N), mais alors on modifierait la variable de la tête de la règle. Il faudrait ensuite s’assurer que N_2 vérifie (nat N_2). Ce terme est vérifiable, mais l’unification qui l’a produite, n’est pas permise dans la méthode de ce message, pour garantir que la règle est respectée. C’est une question en suspend. La méthode décrite dans ce message semble correcte dans les limites de sont applicabilité, mais elle ne s’applique à pas tout. Exactement, elle n’est applicable que quand la forme du terme posé en hypothèse est autant ou plus générale que la forme des têtes de règle représentant les cas. C’est déjà un pas quand‑même. La solution pour la compléter devrait normalement être une réponse à la question de savoir comment à l’appliquer à une hypothèse de plusieurs termes en conjonction et à la question de justifier l’éventuelle exclusion de certains cas. Pour rappel, la mise en œuvre de plusieurs choses décrites ces derniers jours, n’a toujours pas été réalisée, des choses étant en court de réécriture avant de pouvoir les réaliser, tout en devant concevoir des solutions aux questions qui se posent. Les message de ces derniers jours, sont seulement des investigations, ils ne sont pas confirmés par des formulations réels et fonctionnels.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
|
|
|
Administrateur
|
Le problème à résoudre peut être reformulé d’une manière plus générale que dans le précédent message. Cette formulation plus générale se comprend facilement, mais ne laisse pas voir de solution immédiate.
Avant, la description d’une piste à ne pas prendre. Elle ne ferait que poser un nouveau problème, intéressant, mais sans intérêt pour le moment et dont la solution semblerait même encore plus lointaine. Quand en unifiant une hypothèse avec la tête d’une règle, et que l’unification lierait une variable de la tête de la règle (seulement, ce n’est pas à propos des autres cas), il serait possible de considérer que le terme de l’hypothèse restreint la règle. Une restriction, ça peut faire penser à un terme supplémentaire ajouté au corps de la règle. Une idée semblerait alors de faire comme dans le précédent message, de poser le corps de la règle en hypothèse, puis d’unifier l’hypothèse initial à la tête de cette règle, mais en liant les variables de l’hypothèse aux termes de la tête de la règle au lieu de dans l’autre sens, et seulement ensuite, en ajoutant un terme à l’hypothèse représentant le cas, pour ajouter la contrainte de cette autre manière. Un exemple sera plus clair. Précédemment, cet exemple de cas problématique avait été pris : l’hypothèse ⟦(nat (s (s N)))⟧ pour laquelle on souhaiterais la branche de cas correspondant à la règle (nat (s N)) : (nat N). Il a été dit que l’hypothèse ne peut pas être unifiée avec la tête de la règle, parce qu’il faudrait lier le N de l’instance de la règle, N_2, avec le terme interne (s N) de l’hypothèse. Mais il serait possible de ne pas modifier les termes existant de la règle par cette liaison et de plutôt ajouter un terme à l’hypothèse représentant le cas. Le résultat serait alors l’hypothèse ⟦(nat N_2)⟧ & ⟦(eq N_2 (s N))⟧, pour représenter ce cas de l’hypothèse d’origine. Ça ramènerait à résoudre le problème de savoir si étant donné un terme ajouté au corps d’une règle, l’ajout est neutre, restreint seulement la règle mais en la laissant satisfiable ou la rend insatisfiable. La réponse serait nécessaire pour savoir si c’est une branche à effectivement couvrir. Si la réponse est que ça rend la conjonction insatisfiable, alors ce n’est pas une branche à couvrir. La question pourrait éventuellement avoir une utilité, mais elle n’en a aucune maintenant et surtout, c’est trop pour seulement ensuite pouvoir espérer résoudre la question initiale. De plus, le seule terme ajouté porterait toujours sur la relation eq, ce qui au feeling me semble être un mauvais signe, mais je ne vais pas essayer de plus décrire cette impression. L’autre piste, passe par une reformulation. Elle n’apporte pas plus de solution, mais au moins, ne s’égare pas, contrairement à la mauvaise idée du précédent paragraphe. Dans le message précédent, la solution n’est pas toujours applicable, mais elle est parfois applicable quand‑même. En fait, elle correspond à un cas particulier mais peut‑être pas sans intérêt en pratique, celui où l’hypothèse représente un ensemble de règles, plutôt qu’un terme ou une conjonction quelconque. Les justifications de cette solution ont beaucoup insisté sur la validité du corps de la règle posée en hypothèse représentant un cas d’une hypothèse d’origine. Cette validité repose sur la supposition que la règle dont est tirée un cas, est‑elle même satisfiable. C’est pour préserver son caractère satisfiable, que les variables de la tête de la règle ne doivent pas être liées autrement qu’elles ne le sont par le corps de la règle posé en hypothèse. La satisifiabilité est à la base de la reformulation mentionné au début du message, mais cette satisfiabilité doit être contextualisée. C’est aussi une réponse théorique (car sans solution pour le moment) à la génération de la liste de cas à couvrir. La reformulation. Si une hypothèse est unifiable avec la tête d’une règle et que le corps de la règle tel qu’il est après l’unification de la tête, est satisfiable, alors le corps de la règle représente un cas à couvrir. Chaque règle doit être ainsi testée pour l’hypothèse d’origine dont on veut couvrir les cas. C’est aussi simple que ça, en théorie au moins. En pratique, ça pose le problème de pouvoir vérifier la satisfiabilité de n’importe quel corps de règle, dans la foulée de la génération de la liste des cas à couvrir. Dans le message précédent et avant, les hypothèses désignaient toujours des règles telles‑quelles : l’hypothèse contenant toujours un seul terme dont la forme est autant ou plus générale que la forme des têtes de règle pouvant lui correspondre. Il était alors supposé qu’il suffit de sélectionner les règles dont la tête correspond, étant supposé que toutes les règles du système de règles, sont satisfiables. La condition de correspondance avec la tête, élimine les cas à ne pas couvrir, et la garantie que les règles ont toutes été vérifiées satisfiables, garantie que les cas sélectionnés comme à couvrir, sont bien des cas valides. Aucun cas valide n’est omis (préservation de la généralité), et aucun cas sélectionné n’est invalide (pas de risque de faux échecs). Mais ça ne fonctionne plus avec une hypothèse dont le terme peut être quelconque (et encore moins avec une conjonction comme hypothèse), par exemple être plus spécifique que la tête d’une règle. On pourrait se dire qu’il suffirait de se reposer sur la preuve à priori que l’hypothèse est satisfiable et utiliser la règle utilisée pour prouver l’hypothèse, pour produire un cas unique. Mais justement, le problème est que le cas n’est pas nécessairement unique. En fait, il y a une différence entre prouver la satisfiabilité d’une règle et prouver la satisfiabilité d’une hypothèse. Le processus est le même, mais les conclusions qu’on peut ou devrait pouvoir en faire, ne sont pas les mêmes. On peut prouver que les deux règles de la relation nat sont satisifiables, en associant à chacune un exemple de satisfaction. Mais donner un exemple de satisfaction à une hypothèse, garanti seulement que l’hypothèse est satisfiable, sans dire exhaustivement par quelles règles elle peut l’être. Ors, ce serait nécessaire pour avoir la certitude de couvrir tous les cas, sans quoi la couverture des cas n’est pas cohérente, car ne préserve pas la généralité que représente l’hypothèse. Ors, on pourrait par exemple prouver que ⟦(nat N)⟧ est satisfiable, avec la première règle nat, sans pouvoir savoir qu’elle peut être satisfaite par la seconde règle aussi. La preuve de la satisfiabilité d’une hypothèse, ne dit rien sur l’ensemble des règles pouvant la satisfaire. C’est justement le problème qui se pose avec une hypothèse comme ⟦(nat (s (s N))⟧, qui ne désigne pas une ou des règles telles‑quelles. Pour résoudre ce problème, il faudrait que la preuve d’une hypothèse se fasse en prouvant que telles règles peuvent satisfaire l’hypothèse et que toutes les autres règles ne le peuvent pas, ce qui devrait être prouvé aussi. Il faudrait apparemment résoudre le problème de la négation, qui justement nécessite que soit résolu le présent problème d’abord. Ceci dit, la solution du précédent message reste valide quand‑même, même si elle ne couvre pas toutes les possibilités et ne permet la couverture des cas qu’avec les hypothèses ayant une forme adéquate. Mais comme elle ne couvre pas tous les cas, elle ne peut pas permettre de prouver tout ce qui devrait pouvoir l’être et par là, de ne pas prouver toutes les négations non‑plus, comme prouver une négation nécessite une couverture des cas. Ou peut‑être la solution du précédent message est‑elle un cas de base qui permettrait d’avancer ensuite ?  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
« Normalement », la réponse ne peut être que négative. Si la réponse était autre, le problème des récursions infinies ne se poserait pas.
La solution de l’avant dernier message pourrait être conservée, avec juste une petite modification : l’unification avec la tête de la règle se ferait normalement, c’est à dire sans tenir la tête de règle pour constante. Si aucune variable de la règles n’est liée par cette unification, la suite se passe comme dans l’avant dernier message. S’il est détecté qu’elle modifie des variables apparaissant dans la règle, à priori, la couverture des cas est considérée comme non‑réalisable, à moins que la satisfiabilité de la règle ne soit vérifiée avec ses variables ainsi liées, mais seulement s’il est garanti que cette vérification se termine. Ce peut être le cas si le corps de la règle ne contient que des termes faisant référence à des règles dont le corps est vide. La dernière condition permet d’éviter les échecs de couverture de cas dans des situations où ce serait difficilement acceptable, tant ce serait humainement incompréhensible. Un exemple serait le cas où au lieu d’écrire « (r c). », il serait écrit « (r V) : (eq V c). ». Les deux sont équivalentes, mais sans la petite touche de la fin du précédent paragraphe, la seconde règle ferait systématiquement échouer le génération de la couverture de cas. Comme dans l’avant dernier message, si la règle est vérifiée satisfiable, le corps de la règle est posé comme une hypothèse, avec toutes les variables représentant des généralités. La seule différence, serait dans cette vérification sous condition qu’il soit garanti qu’elle se termine et dans un temps raisonnable. Il est possible d’aller plus loin, mais ce ne sera pas décrit ici, pour rester un minimum accessible, alors que ça ne me semble déjà pas l’être autant que ça le devrait. C’est au minimum censé permettre d’avoir conscience et un minimum de compréhension, de ce que signifie concrètement, faire des vérifications portant sur des généralités, c’est à dire faire des démonstrations. La couverture des cas pour une conjonction, pourrait se faire en générant une combinaison des couvertures possibles pour chaque terme. Mais fait de cette manière automatique, le nombre cas à couvrir pourrait vite augmenter. Par exemple avec seulement trois termes, si le premier a quatre cas possibles, le second cinq et le troisième, six, la couverture est déjà composée de 120 cas possibles, sous chacun desquels doit être vérifiée une requête ou le corps d’une règle, pour conclure à sa vérification avec des généralités. C’est encore sans compter l’éventuel découpage en cas de chacun de ces cas eux‑mêmes. La vérification automatique dans ces conditions, devrait se faire avec des limites, par exemple une limite du nombre de cas générés automatiquement, au delà de quoi, une intervention humaine serait requise pour faire les bons choix nécessaires à la démonstrations. Sans ça, une vérification automatique pourrait vite avoir à faire des couvertures avec des nombres de cas à plusieurs zéros, pour une seule vérification d’un terme avec une hypothèse non‑triviale. Il faut espérer que la méthode de base décrite dans l’avant dernier message et affinée dans celui‑ci, soit suffisante pour des vérifications intéressantes et utiles, au moins pour que le système de base ne soit pas trop excessivement compliqué à démontrer. Il apparaît que la couverture des cas, est une source de difficultés plus importante qu’attendue. Je m’y attendais, mais quand‑même pas à ce point. La négation, qui est liée à cette question, pose encore plus de problèmes. Pas seulement parce que prouver la négation nécessite assez rapidement une couverture des cas, mais aussi parce que son cas de base, qui se constate pendant l’unification, n’est pas évident à propager. Un exemple pour que ce soit plus clair : soit une règle A : B & C & D. Disons que le terme C est vérifié et que la tentative d’unification échoue avec toutes les têtes de toutes règles. Dans ce cas, la contradiction est avérée. Mais jusqu’où remonter cette contradiction ? Si la cause de l’échec est une liaison de variable par la vérification du terme B, peut‑être qu’une autre solution pour B résoudra le problème et dans ce cas, il ne faut pas conclure à l’échec inconditionnel de cette instance de règle avec ses liaisons initiales. Si au contraire, la liaison à l’origine de l’échec systématique, est extérieur à cette instance de cette règle, alors on peut conclure à la négation de cette instance de cette règle, dans tous les cas. Ce n’est pas trivial à première vue (peut‑être une idée s’énonçant bien, mais sans certitude et qui ne sera pas réalisée avant un certain temps), et ça vient s’ajouter à la difficulté venant avec la couverture des cas, une couverture que nécessiterait souvent aussi la négation. Pour la couverture des cas, même si une solution plus complète est conçue (peut‑être déjà une idée, mais sans certitude), ce ne sera pas rapporté ici, parce que ce serait probablement trop compliqué à exposer dans ce sujet au point de le rendre trop difficile à lire. Normalement, il n’y aura pas de retour sur cette question. Il y aura peut‑être un retour sur la question de la preuve de la négation, si est trouvée une solution assez intéressante et pas trop complexe, même si elle ne s’applique pas toujours (à la manière de la solution incomplète mais assez intéressante, proposée pour la génération des cas à couvrir). Un retour sur cette question, n’est pas exclus, mais pas garanti non‑plus. Une petite note sur une question de vocabulaire. Je me souviens avoir assez souvent lu l’expression “ cases split ”, peut‑être surtout dans la littérature à propos de l’assistant de démonstration, Coq. Cette expression est compréhensible, mais je la trouve trompeuse. D’abord, il n’y a pas nécessairement plusieurs cas, il peut autant bien n’y en avoir qu’un seul. Ensuite, la raison pour laquelle cette notion a été introduite, était surtout pour résoudre le problème de l’opacité des hypothèses, elles‑mêmes initialement introduite pour représenter les généralités. La raison initiale était de les rendre plus transparentes quand ça peut être nécessaire, la notion de couverture des cas étant plus le moyen que l’intention. Pour ces deux raisons, je me demande si parler d’ouvrir une hypothèse, comme on ouvre une boite, plus proche de l’intention, ne serait pas plus évocateur et moins trompeur. Cette fois, je crois qu’il sera vraiment pris congé de ce sujet pendant un temps, parce que la petite montagne de difficultés qui s’est élevé avec les deux dernières questions, suggère de prendre du recul et de n’y revenir qu’après avoir laissé décanter et à tête reposée.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Hibou a écrit : […] Après ce message, ce sera vraiment‑vraiment. C’est avec le langage naturel qu’on comprend le mieux les choses, mais seul un langage formel peut rendre les choses vérifiables selon un procédé tout aussi formellement établit. Voici un exemple de compléments au langage qui a été défini jusqu’ici. C’est seulement une ébauche, une base, il n’a pas encore été mis en œuvre. Les exemples ci‑dessous ajoute au langage, la possibilité de prouver qu’une règle est satisfiable, de justifier une hypothèse, de lister ses cas et de faire des démonstrations d’après une hypothèse opaque ou d’après une hypothèse après son ouverture. L’exemple est découpé en parties, chacune étant commentée. Code :§nat-z (nat z). C’est la reprise des règles qui ont servi d’exemple (il manque juste la règle eq, qui pose une petite colle). Comme avant, les §n servent à donner des noms aux règles, mais ici, aussi aux hypothèse. Le symbole =| est le |= orienté dans l’autre sens. On peut lire A =| B comme B est une solution de A ou B satisfait A. C’est une notation pour la satisfiabilité dont il a été souvent question. La satisfiabilité pourrait se faire avec des termes constants, mais comme les hypothèses représentent des généralités qui sont comme des ensembles de constantes, elles sont utilisés à la place comme une preuve de satisfiabilité plus général. En gros, A : B =| §h peut se lire l’existence de §h prouve que A : B est satisfiable. La satisfiabilité des hypothèses aussi, doit être montrée. Mais le symbole =| n’est pas utilisé. La raison est que c’est plutôt le terme de l’hypothèse qui est satisfiable. Aussi, comme une hypothèse peut avoir plusieurs justifications et qu’une liste exhaustive de ses justifications peut correspondre à la liste de ces cas possible, il est considéré qu’on peut dire par abus de langage, que la liste des cas d’une hypothèse est un peu sa définition. Pour cette raison, la justification des hypothèse est noté avec le même symbole que les règles qui sont prises pour des définitions. Par exemple ⟦H⟧ : §r1 | §r2, signifie que l’hypothèse a deux cas possibles, qui sont les règles §r1 et §r2 et la liste de ces cas fait en même temps office de preuve que le terme de l’hypothèse est satisfiable ; deux en un. Plus haut, on peut remarquer que les preuve de satisfiabilité des règles, se font en désignant des hypothèses, et que à l’inverse, les preuves de satisfiabilité des hypothèse qui est aussi la liste de leurs cas, se font en désignant des règles. Cette notation rend visible la relation réciproque entre les deux. Certaines hypothèses peuvent être justifiées plusieurs fois, c’est normal, dans ce cas, elles sont complétés par de nouveaux cas et reçoivent un nouveau nom. Elles pourraient avoir le même nom dans tous les cas, mais donner un nom différent rend plus clair qu’elles sont complétées avec l’introduction de règles pouvant leur correspondre. Chaque ligne ne dépend que des précédentes, que ce soit pour les hypothèse ou les règles, c’est ce qui explique que la règle §poly-p n’est pas justifiée par elle‑même, même si elle pourrait l’être si elle était posée une seconde fois. Code :VERIFY (int Z) : ⟦(int-z Z)⟧. C’est un exemple de preuve, la vérification qu’un Z qui vérifie int-z vérifie toujours int ; l’exemple sur lequel la vérification automatique avait séchée et qui a nécessité une réécriture pour être vérifié. Ce cas est celui qui avait fait conclure que l’opacité des hypothèse empêche certaines vérifications, ce qui a amené à introduire la notion d’ouverture de l’hypothèse et de cas représentant l’hypothèse. Les mots en majuscules sont censées être des mots clés. La ligne commençant par YIELDS, correspond à l’unification de l’hypothèse avec la tête d’une règle correspondant à un cas. Ici, il n’y a qu’un cas. Comme expliqué précédemment, la variable Z est lié, le corps de la règle est posée en hypothèse et une hypothèse dérivée remplace l’hypothèse d’origine. Le symbole -| est le symbole |- orienté dans l’autre sens. On peut lire A -| B comme A est justifié ou produit par B. Le B peut être l’instanciation d’une règle, la vérification d’une règle, la liste n’étant pas exhaustive. Le IN signifie dans le contexte de. Par exemple §3 IN §2 signifie la règle rapportée en §3 vérifiée dans un contexte où on a l’hypothèse rapportée en §2. Ces explications sont déjà un peu longues à lire, alors pas plus de détails ne sont donnés, mais ils peuvent se deviner en essayant de suivre. La preuve plus haut n’avait pas put être faite avec la simple requête « ⟦(int-z Z)⟧ & (int Z) ? », parce que la vérification nécessite d’ouvrir l’hypothèse, qui autrement ne vérifie rien d’utile à la démonstration. La requête s’était achevé sans résultat. Mais cette variante, s’était achevé avec une solution : ⟦(nat N)⟧ & (int-z (i N N)) & (int (i N N)) ? », où on peut reconnaître dans la requête, l’hypothèse utilisée dans la démonstration plus haut. Code :VERIFY (nat-lt N (s (s N))) : ⟦(nat N)⟧. C’est un exemple avec deux branches. Il se trouve que les deux branches sont identiques, parce que le point de départ de chacun des cas ne change rien au raisonnement qui est le même dans les deux branches. En fait, ce raisonnement peut se faire sans ouvrir l’hypothèse, ce qui rend moins étonnant que les deux branches soient identiques. Code :VERIFY (nat-lt N (s (s N))) : §1 ⟦(nat N)⟧. La même chose, mais sans ouvrir l’hypothèse, en raisonnant avec l’hypothèse sous sa forme opaque ou abstraite, directement. Que l’hypothèse n’ait pas besoin d’être ouverte, explique que cette vérification avait put être faite avec une requête ordinaire : « ⟦(nat N)⟧ & (nat-lt N (s (s N))) ? », qui avait renvoyé une unique solution, correspondant en fait à la preuve plus haut.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
La logique ne dit pas ce que les choses sont, elle dit ce qui est et ce
qui n’est pas ; et encore, seulement pour les questions qu’on lui a posé (si encore elle peut y répondre).  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Une possible compréhension des choses, peut être à corriger, mais ça doit être à peu près ça.
Tout comme le « vrai » ne peut désigner autre chose que lui‑même, entre autres pas le « faux », tout comme le « faux » ne peut désigner que lui‑même, entre autres pas le « vrai », une expression ne doit avoir qu’un seul sens désigné (même s’il peut être désigné de plus d’une manière). On peut tirer des conclusions du sens désigné ; dans le langage courant on parlerait aussi bien de signification dans le premier cas que dans le second cas, mais ce n’est pas la même chose, sinon le sens, plus explicitement, le sens désigné, ne serait pas fiable, c’est à dire que le sens (celui de la sémantique) serait vain. C’est au moins le cas de la sémantique qui intéresse la logique (dans d’autres domaines, soit c’est à nuancer, soit c’est plus confus ou joueur ou manipulateur). C’est là qu’est la principale utilité de la notion de type, qui est un moyen de restreindre l’écriture d’une manière qu’elle ne puisse pas utiliser un sens en lieu et place d’un autre, ce que la syntaxe seule permettrait, à moins qu’elle ne soit déjà restreinte d’une manière qui ne lui permet pas de formuler à propos de tous les concepts eux‑mêmes, de sa propre sémantique, ce qui est quand‑même parfois le cas. Dans ce cas, le type est implicitement garanti par la syntaxe, mais une syntaxe dont l’expressivité a alors des limites.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Ce message est déroutant, dans le contexte de ce qui a été dit l’année précédente. Il est déroutant, mais ne semble pour le moment pas incohérent. Il pose des questions qui étaient latentes, avaient été mises de côté mais qui ont resurgit et sont donc maintenant posées visiblement. En plus d’être déroutant, ce message est aventureux, il peut être lu pour être oublié ensuite, s’il ne convainc pas. Il y a ici, une part de raison formelle et une part de raisons pratiques mises en balance.
Une distinction avait été soulignée, entre les termes les plus externes, désignant des relations et les termes internes, désignant des expressions qui avaient été comparées à des constructeurs, au sens de ceux de SML par exemple. Il avait aussi été souligné que la constante par laquelle commence un terme, qu’il soit interne ou le plus externe, ne peut jamais être captée par une variable. Ici, il est envisagé de nettoyer le langage, en remettant le second point en question et en soulignant que cette constante par laquelle commence toujours un terme, n’est pas d’une nature différente des autres constantes, justifiant de ne pas la distinguer syntaxiquement. C’est finalement un retour à une idée initiale qui avait rapidement été mise de côté, par prudence. Un large partie de ce qui est dit dans ce message, se place en amont de la question du message précédent, celle d’introduire une notion de type pour qu’une chose ne puisse pas subitement en désigner une autre, ce qui serait une incohérence. L’incohérence est définie comme pouvoir conclure par exemple que x = y, où x et y sont deux constantes différentes, ce qui serait le cas en particulier, si on concluait que Vrai = Faux. Une autre partie se place en même temps que se pose la question d’introduire une notion de type. Les questions re‑posées dans ce message, ont précisément resurgit en pensant à cette notion de type, et à quoi elle devrait s’appliquer. La question est venue de savoir quel est le type de la constante initiale commençant chaque terme, comme elle a syntaxiquement un status particulier. C’est en cherchant à savoir ce qui la distingue, qu’il a été conclut que rien ne la distingue des autres et que la règle syntaxique la distinguant, peut être relaxée. Mais ce n’est pas sans poser des questions. D’abord une remise en question de l’analogie comparant ces constantes à des constructeurs. L’année précédente, il avait déjà été noté que bien qu’il y ait des similitudes, les termes du langage dont il est question ici, sont moins contraints que les constructeurs de SML. En fait, ce ne sont pas des constructeurs, et l’analogie ne vaut que pour comme une manière de partiellement les comprendre ; cette analogie est d’un autre côté, en partie incorrecte. Reprenons l’exemple des entiers naturels, formulés avec ces deux règles : (nat z). (nat (s N)) : (nat N). L’analogie faisait voir z comme un constructeur sans argument et s comme un constructeur prenant un unique argument de type nat. Mais rien n’empêche d’écrire un terme tel que (s abcd), qui ne vérifiera juste pas la règle nat. Ce rappel est pour souligner que ni s ni z, n’ont un type, au sens d’un type de données. Seule la règle nat dit de quelle manière elle attend que ces constantes soient utilisées dans des termes ; mais même s’il ne serait pas vérifié par la règle nat, ça n’empêcherait pas qu’une règle vérifie un terme comme (s abcd), même une règle n’ayant pas de rapport avec les entiers naturels. Ce qu’il faut comprendre par là, c’est que z, (s z) ou (s (s z)) ou (s abcd), ne sont que des symboles, sans signification intrinsèque (peut‑être que ça avait déjà été expliqué, ça le rappellera alors), leur seule particularité étant d’avoir une structure décomposable ; c’est à dire que par unification, on peut « lire » un terme, comme (s (s z)) avec un terme comme (s A), qui liera A à (s z). On peut vérifier que par exemple, s, n’a rien de magique, au point de pouvoir s’en passer : (nat z). (nat (z N)) : (nat N). Un ensemble de solution serait : N = z N = (z z) N = (z (z z)) N = (z (z (z z))) … La constante s peut donc s’appeler z, en laissant les règles équivalentes, pour ce qui est de l’interprétation des termes qu’elles vérifient. Ça fait échos à ce qui avait été dit d’une définition de l’égalité : (eq A A). Il avait été dit que ce n’est pas son nom, eq, qui fait de cette règle, une définition de l’égalité, que c’est sa structure, qui en fait une définition de l’égalité. Avec un bémol qui viendra rapidement après, il est même possible d’imaginer deux exemples, pour le moment syntaxiquement incorrecte, mais ayant intuitivement du sens, se passant des constantes s, z et eq. Les entiers naturels pourraient être être représentés comme suit : (nat ()). (nat (N)) : (nat N). N = () N = (()) N = ((())) N = (((()))) … La définition de l’égalité pourrait être représentée comme suit : (A A). Elle serait vérifiée par (x x), (y y), etc. Quelle serait la différence entre (eq A A) et (A A) ? Pour les paires d’argument qui les vérifieraient, il n’y aurait pas de différence. Maintenant, imaginons que cette règle existe conjointement à une règle presque quelconque, à deux termes, disons (r X), dont X = r serait une solution. Dans ce cas, (r r), vérifierait à la fois la règle (A A) et la règle (r X). Mais dans le corps d’une règle, un terme comme (A B) pourrait devenir ambiguë, … ce qui n’est pas la même chose que incohérent. Seulement, de telles ambiguïtés sont aussi possible avec des règles dont le terme commence par une constante. Maintenant imaginons que (A A) existe conjointement à d’autres règle, qui sont toutes à trois éléments ou plus. Dans ce cas, le terme (A B) dans le corps d’une règle, n’est plus ambiguë, l’arité suffit à elle seule à distinguer la règle exacte et donc la signification du terme. Tout ça peut ressembler à de l’errance, mais souligne au moins, que le point important, est de pouvoir distinguer des termes ou pas et que la possibilité de faire cette distinction, ne nécessite pas nécessairement que le terme commence par une constante. Comme déjà rapidement suggérée l’année précédente, cette constante pourrait même se trouver ailleurs que en première position du terme. Toujours pour prendre une exemple pour le moment syntaxiquement incorrecte, au lieu d’être (eq A A), le terme pourrait être (A eq A). Là encore, s’il existe par ailleurs une règle (r A B) dont A = eq et B = r serait une solution, alors (r eq r) serait une solution aux deux règles. On peut deviner que la question, est surtout une question de convention et d’organisation. Je crois que la règle posant qu’un terme commence toujours par une constante, est justement une convention, imposée par une règle syntaxique, mais dans le fond, seulement une convention, pas une nécessité formelle. C’est une possibilité de choix : je crois qu’il peut être utile de séparer ce qui est formellement requis de ce qui est jugé préférable en pratique et dont on fait une convention, pour des raisons pratiques. Les conventions qui ne sont pas indiscutables, peuvent être séparées de la définition du langage. La définition de l’égalité est un cas particulier, on peut trouver même plus épuré, de l’écrire (A A) plutôt que (eq A A) ou (A eq A), la constante eq étant arbitraire et non‑nécessaire, et (A A) représentant bien l’égalité le plus purement. Pourtant, à côté de la raison pratique, on peut avoir une raison plus forte, de la nommer explicitement, mais cette raison n’existe que dans le cas où un terme peut commencer par une variable, une possibilité qui cette fois a une raison formelle. L’année précédente, avait été fait remarquer que le fait qu’un terme commence toujours par une constante, empêche de faire une requête sur quelles règles vérifient un ou des termes. Par exemple étant donné une règle (x A B) et une règle (y A B), il n’est pas possible de formuler une requête comme « (R a b) ? » pour savoir quelles relations « a b » vérifie. Ce dernier point, fait la plus importante raison de relaxer la règle imposant qu’un terme commence toujours par une constate. La liberté de distinguer une règle par une constante ou pas et initiale ou pas, est secondaire en comparaison, mais cette liberté là vient automatiquement avec, et comme vu plus haut, il faut penser aux conséquences qu’elle peut avoir. Une question juste un peu moins importante, est aussi de ne pas distinguer syntaxiquement, des choses qui ne se distinguent pas formellement, sémantiquement. La question du type, s’est invité aussi dans la distinction entre termes internes, et termes externes. Les seconds sont des termes désignant une règle et alors sujet à substitution, pas les premiers, qui ne sont sujet qu’à unification, seulement. Q’un terme puisse commencer par une variable, implique qu’un terme tout entier puisse être une variable. Là vient la question la plus délicate, celle d’une variable se trouvant en position d’un terme externe et en même temps ailleurs, en position d’un terme interne. Que penser de cet exemple fictif de règle : (r1 A) : A & (r2 A). Le plus important est dans le corps de la règle, c’est à dire la seconde et la troisième occurrence de A. La seconde occurrence de A, désigne une tête de règle, pas sa troisième occurrence. Cette possibilité est plus inquiétante. Une conclusion a déjà été posée pour ce cas, mais cette conclusion est inattendue, au point qu’il est préférable d’attendre avant de l’exposer, peut‑être après l’avoir révisée. Ce sera donc pour plus tard.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Hibou a écrit : […] En étant implicite, ce que j’avais écrit a de quoi sembler trop exagéré. C’était en pensant que c’est la relation qui fait le sens du terme. Ce ne sont pas que des symboles sans aucune signification, même si elle doit être confirmée par la relation, ils ont au moins un sens potentiel. Sens potentiel, parce qu’ils peuvent en avoir plusieurs, rien n’empêchant un terme de vérifier plus d’une relation. Ici, deux idées du sens se rencontrent : celui des termes du point de vu du langage lui‑même et celui des termes du point de vu de l’interprétation faite des termes, au delà du langage. Cette remarque est peut‑être la clé de la question sur laquelle se terminait le message précédent, mais c’est pour plus tard.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Hibou a écrit : […] Il ne faut pas comprendre que ça sous‑entendrait que cette convention est mauvaise, je la trouve au contraire bonne, excepté pas dans tous les cas. Le problème est que la forcer par une règle de la syntaxe, a des effets secondaires limitant l’expressivité du langage. Une idée qui sera présentée encore plus tard, confirmera que cette convention est bonne, mais ne dira pas plus qu’elle devrait être forcée par la syntaxe. Une autre utilité de la mettre en question, est que ça permettra de la justifier dans un cas, avec une raison explicitement donnée, même si ça aura été en donnant aussi une raison de ne pas la forcer.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
Administrateur
|
Hibou a écrit : […] Ceci, parce que les deux utilisations de z, se distinguent par leurs arités. Le z de la première règle et le z de la seconde règle, ont le même nom, mais ne sont « pas les mêmes ». Hibou a écrit : […] Une ambiguïté qui pourrait être problématique quand‑même. Le cas où un terme vérifie les deux règles en même temps, est le moins pire de tous. Le pire est le cas où il n’est pas clair de savoir laquelle des deux règles il vérifie. Par exemple (A B) pourrait vérifier (r X) alors qu’en le lisant on penserait peut‑être plus facilement qu’il vérifie (A A). Ce n’est pas formellement une incohérence (d’après la définition de l’incohérence donnée précédemment, jusque maintenant) ; mais c’est tout comme une incohérence, comme cela sera formellement le cas, avec une définition plus complète de l’incohérence, qui sera donnée plus tard.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |
|
|
|

