Cette partie du forum n’est pas compatible avec les bloqueurs publicitaires
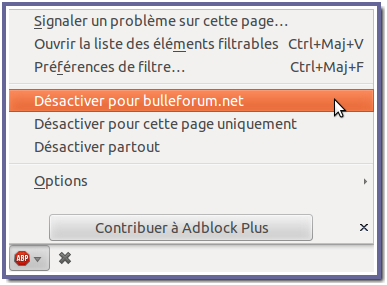
Félicitations à vous, de préférer les accès payants plutôt que la gratuité par la publicité, c’est honnorable et cohérent de votre part. Malheureusement, l’accès payant par micropaiement (qui serait d’environ 1 cent pour 20 pages consultées) n’est pour l’instant pas encore mis en place, et l’accès gratuit sans publicité, est réservé aux membres actif(ve)s du forum. En attendant, si vous souhaitez poursuivre votre visite chez nous, vous pouvez ajouter le site à votre liste blanche, ou encore mieux, désactiver le bloqueur partout. Pour ajouter le site à votre liste blanche, pour Firefox (similaire pour les autres navigateurs), rendez‑vous en bas à gauche de la fenêtre de votre navigateur, et cliquez sur le menu comme dans l’exemple de l’image ci‑dessous, puis rechargez la page, en appuyant sur F5.
|
|
|
| Auteur | Message |
|---|---|
|
Administrateur
|
La playlist d’une série en vidéo sur les nombres complexes : Imaginary numbers are real — Welch Labs (youtube.com).
Les nombres complexes sont des objets algébriques. Ils ont une représentation en deux dimensions, mais ne sont pas des vecteurs. Avec les vecteurs, les deux composantes sont indépendantes, d’où l’adjectif « orthogonales » pour parler de choses pouvant varier librement l’une par rapport à l’autre. Avec les complexes, les deux composantes sont liées. Un nombre complexe n’est pas non‑plus une sorte de matrice à deux cellules. Les nombres complexes sont parfois la seule solution dans les étapes de calcul, pour passer d’une problème dans les réels à une solution pourtant dans les réels aussi. C’est le cas avec la résolution d’équations du troisième degré dans les réels. Sans les nombres complexes, l’algèbre ne serait pas complète, car elle ne serait pas stable (closed, en Anglais) pour l’opération que sont les racines.  Hibou57 « La perversion de la cité commence par la fraude des mots » [Platon] |

